Умножение матрицы на число c. Действия с матрицами

Умножение матриц.

Умножение матриц – это одна из самых распространенных операций с матрицами. Матрица, которая получается после умножения, называется произведением матриц.

Произведением матрицы A_m×n на матрицу B_n×k будет матрица C_m×k такая, что элемент матрицы C, находящийся в i-ой строке и j-ом столбце, то есть элемент c_ij равен сумме произведений элементов i-ой строки матрицы A на соответствующие элементы j-ого столбца матрицы B.

Процесс умножения матриц возможен только в случае, когда число столбцов первой матрицы равно числу строк второй матрицы.

Пример:
Можно ли умножить матрицу 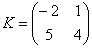на матрицу ?

m = n, значит, умножать данные матрицы можно.

Если же матрицы поменять местами, то, при таких матрицах, умножение уже не будет возможно.

m ≠ n, таким образом, выполнять умножение нельзя:

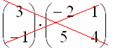
Довольно часто можно встретить задания с подвохом, когда ученику предлагается умножить матрицы, умножение которых заведомо невозможно.

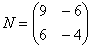Обратите внимание, что иногда можно умножать матрицы и так, и так. К примеру, для матриц, и возможно как умножение MN, так и умножение NM.

Операция умножения матриц.

Операция умножения матриц – это не очень сложное действие. Умножение матриц лучше понимать на конкретных примерах, т.к. только определение может сильно запутать.

Начнем с самого простого примера:

Необходимо умножить 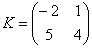на . Первым делом приведем формулу для данного случая:

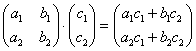– здесь хорошо прослеживается закономерность.

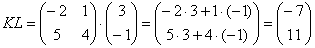
Далее более сложный пример:

Умножить на .

Формула для этого случая: .

Умножение матриц и результат:

В результате получена т.н. нулевая матрица.

Очень важно помнить, что здесь не работает «правило перестановки мест слагаемых» так как почти всегда MN ≠ NM. Поэтому, производя операцию умножения матриц их ни в коем случае нельзя менять местами.

Теперь рассмотрим примеры умножения матриц третьего порядка:

Умножить 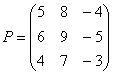на .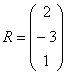

Формула очень похожа на прошлые:

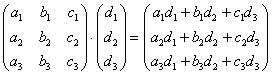
Решение матрицы: .

Умножение матрицы на число.

Умножение матрицы на число – это тоже самое умножение матриц, только вместо второй матрицы берется простое число. Как можно догадаться, такое умножение выполнять гораздо проще.

Пример умножения матрицы на число:

Тут все понятно – для того, чтобы умножить матрицу на число, необходимо каждый элемент матрицы последовательно умножить на указанное число. В данном случае – на 3.

Еще один полезный пример:

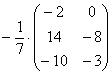– умножение матрицы на дробное число.

Первым делом покажем то, чего делать не надо:

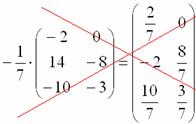
При умножении матрицы на дробное число не нужно вносить дробь в матрицу, так как это в первую очередь только затрудняет дальнейшие действия с матрицей, во-вторых, затрудняет проверку решения преподавателем.

И, тем более, не нужно делить каждый элемент матрицы на -7:

.

Что стоит сделать в данном случае – это внести минус в матрицу:

.

Если бы у вас был пример, когда все элементы матрицы делились бы на 7 без остатка, то тогда можно (и нужно!) было бы поделить.

В данном примере можно и нужно умножить все элементы матрицы на ½, т.к. каждый элемент матрицы делится на 2 без остатка.

Примечание: в теории высшей математики школьного понятия «деление» нет. Вместо фразы «это поделить на это» всегда можно сказать «это умножить на дробь». То есть, деление – это частный случай умножения.

Калькулятор матриц – действия с матрицами онлайн

С помощью калькулятора матриц вы сможете выполнять различные преобразования матриц, решать СЛАУ, а также находить некоторые характеристики, как, например, определитель, след и ранг. Подробнее о функционале и использовании калькулятора смотрите после блока с самим калькулятором.

Транспонирование — операция, при которой строки и столбцы матрицы меняются местами: a T _ij = a_ji

Выполнено действий: 400859

Как пользоваться калькулятором матриц

1. Выберите матрицу (или матрицы) с помощью переключателей ( )
2. Укажите размер с помощью выпадающих списков под матрицей ( × )
3. Заполните элементы (нулевые элементы можно не заполнять.)
4. Выберите в выпадающем списке требуемую функцию и, если требуется, введите дополнительные параметры.
5. Нажмите кнопку .
6. Если вывод чисел не устраивает, просто поменяйте его — доступны три варианта представления: правильные дроби (2

Ввод данных и функционал

• В качестве элементов используются обыкновенные правильные дроби ( 1/2 , 29/7 , -1/125 ), десятичные дроби ( 12 , -0.01 , 3.14 ), а также числа в экспоненциальной форме ( 2.5e3 , 1e-2 ).
• Длина вводимых чисел ничем не ограничена, вводите хоть 1000 цифр, правда, возможно, придётся подождать, пока будут идти вычисления!
• Используйте для работы одну или две матрицы (чтобы выполнять операции с двумя матрицами, передвиньте переключатель второй матрицы).
• Вставляйте результат в A или B с помощью кнопок “Вставить в A” и “Вставить в B”.
• Перетаскивайте (drag-and-drop) матрицы из результата в A или B.
• Используйте стрелки ( ← , ↑ , → , ↓ ) для перемещения по элементам

Что умеет наш калькулятор матриц?

Вычисление выражений с матрицами

Вы можете вычислять различные арифметические выражения с матрицами, а также с результатами некоторых преобразований этих матриц.

Из чего могут состоять выражения?

• Целые и дробные числа
• Матрицы A, B
• Знаки арифметических действий: + – * /
• Круглые скобки для изменения приоритета операций: ( )
• Транспонирование: ^T
• Возведение в целую степень: ^

Примеры корректных выражений

• Cложение двух матриц: A+B , (A)+(B) , ((A) + B)
• Возведение линейной комбинации матриц в степень: (3A – 0.5B)^5
• Произведение транспонированной матрицы на исходную: A^TA
• Обратная матрица в квадрате для B: B^-2

Что такое матрица?

Матрицей размера n×m называется прямоугольная таблица специального вида, состоящая из n строк и m столбцов, заполненная числами. Матрицы обозначаются заглавными латинскими буквами. При необходимости размер записывается следующим образом: A_n×m .

Примеры матриц

Элементы матрицы

Элементы A обозначаются a_ij , где i – номер строки, в которой находится элемент, j – номер столбца.

Некоторые теоретические сведения

Транспонирование — операция, при которой строки и столбцы матрицы меняются местами: a T _ij = a_ji

Главная диагональ квадратной матрицы — диагональ, которая проходит через верхний левый и нижний правый углы. Элементы главной диагонали — a_ii

Единичная матрица E_n×n — квадратная матрица из n столбцов и n строк с единицами на главной диагонали и нулями вне её.

Ранг — это максимальное количество линейно независимых строк (столбцов) этой матрицы. Обозначение: rank(A)

След — это сумма элементов, находящихся на её главной диагонали. Обозначение: tr(A) или track(A)

Умножение матрицы на число — матрица такой же размерности, что и исходная, каждый элемент которой является произведением соответствующего элемента исходной матрицы на заданное число.

Возведение в степень — умножение заданной матрицы саму на себя n-ое количество раз, где n – степень, в которую необходимо возвести исходную матрицу. Обозначение: A n

Обратная матрица A −1 — матрица, произведение которой на исходную матрицу A равно единичной матрице: A -1 ×A = A×A -1 = E

Треугольная матрица — квадратная матрица, у которой выше (верхнетреугольная матрица) или ниже (нижнетреугольная матрица) главной диагонали находятся нули.

LU-разложение — представление матрицы в виде произведения двух матриц L и U, где L — нижнетреугольная матрица с еденичной диагональю, а U — верхнетреугольная матрица. A = L·U

Сложение матриц A_n×m и B_n×m — матрица C_n×m, получаемая попарной суммой соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен: с_ij=a_ij+b_ij

Разность матриц A_n×m и B_n×m — матрица C_n×m, получаемая попарной разностью соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен: с_ij=a_ij-b_ij

Умножение матриц A_n×k и B_k×m — матрица C_n×m, у которой элемент (c_ij) равен сумме произведений элементов i-той строки матрицы A на соответствующие элементы j-того столбца матрицы B: c_ij = a_i1·b_1j + a_i2·b_2j + . + a_ik·b_kj

Математика для чайников. Матрицы и основные действия над ними

Доверь свою работу кандидату наук!

1-й курс, высшая математика, изучаем матрицы и основные действия над ними. Здесь мы систематизируем основные операции, которые можно проводить с матрицами. С чего начать знакомство с матрицами? Конечно, с самого простого – определений, основных понятий и простейших операций. Заверяем, матрицы поймут все, кто уделит им хотя бы немного времени!

Определение матрицы

Матрица – это прямоугольная таблица элементов. Ну а если простым языком – таблица чисел.

Обычно матрицы обозначаются прописными латинскими буквами. Например, матрица A, матрица B и так далее. Матрицы могут быть разного размера: прямоугольные, квадратные, также есть матрицы-строки и матрицы-столбцы, называемые векторами. Размер матрицы определяется количеством строк и столбцов. Например, запишем прямоугольную матрицу размера m на n, где m – количество строк, а n – количество столбцов.

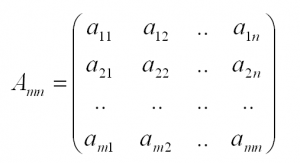
Элементы, для которых i=j (a11, a22, .. ) образуют главную диагональ матрицы, и называются диагональными.

Что можно делать с матрицами? Складывать/вычитать, умножать на число, умножать между собой, транспонировать. Теперь обо всех этих основных операциях над матрицами по порядку.

Операции сложения и вычитания матриц

Сразу предупредим, что можно складывать только матрицы одинакового размера. В результате получится матрица того же размера. Складывать (или вычитать) матрицы просто – достаточно только сложить их соответствующие элементы. Приведем пример. Выполним сложение двух матриц A и В размером два на два.

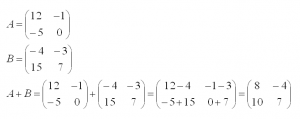
Вычитание выполняется по аналогии, только с противоположным знаком.

Умножение матрицы на число

На произвольное число можно умножить любую матрицу. Чтобы сделать это, нужно умножить на это число каждый ее элемент. Например, умножим матрицу A из первого примера на число 5:

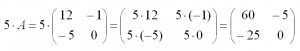
Операция умножения матриц

Перемножить между собой удастся не все матрицы. Например, у нас есть две матрицы – A и B. Их можно умножить друг на друга только в том случае, если число столбцов матрицы А равно числу строк матрицы В. При этом каждый элемент получившейся матрицы, стоящий в i-ой строке и j-м столбце, будет равен сумме произведений соответствующих элементов в i-й строке первого множителя и j-м столбце второго. Чтобы понять этот алгоритм, запишем, как умножаются две квадратные матрицы:

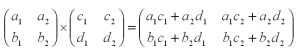
И пример с реальными числами. Умножим матрицы:

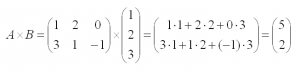
Операция транспонирования матрицы

Транспонирование матрицы – это операция, когда соответствующие строки и столбцы меняются местами. Например, транспонируем матрицу A из первого примера:

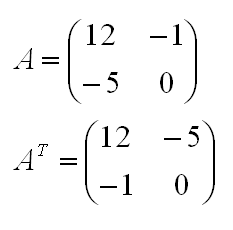
Определитель матрицы

Определитель, о же детерминант – одно из основных понятий линейной алгебры. Когда-то люди придумали линейные уравнения, а за ними пришлось выдумать и определитель. В итоге, разбираться со всем этим предстоит вам, так что, последний рывок!

Определитель – это численная характеристика квадратной матрицы, которая нужна для решения многих задач.
Чтобы посчитать определитель самой простой квадратной матрицы, нужно вычислить разность произведений элементов главной и побочной диагоналей.

Определитель матрицы первого порядка, то есть состоящей из одного элемента, равен этому элементу.

А если матрица три на три? Тут уже посложнее, но справиться можно.

Для такой матрицы значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.

К счастью, вычислять определители матриц больших размеров на практике приходится редко.

Здесь мы рассмотрели основные операции над матрицами. Конечно, в реальной жизни можно ни разу так и не встретить даже намека на матричную систему уравнений или же наоборот – столкнуться с гораздо более сложными случаями, когда придется действительно поломать голову. Именно для таких случаев и существует профессиональный студенческий сервис. Обращайтесь за помощью, получайте качественное и подробное решение, наслаждайтесь успехами в учебе и свободным временем.

Умножение матрицы на число c. Действия с матрицами

Сложение определено для матриц одного типа, т.е. для матриц, у которых число строк и столбцов совпадает. Сумма матриц (A=>) и (B=>), матрица (A+B), определяется следующим образом: ((A+B)_=A_+B_), (1 leq i leq m, 1 leq k leq n). Иными словами: складываются элементы матриц (A) и (B), стоящие на одинаковом месте (т.е. на пересечении одинаковых строк и столбцов) и записываются в то же место.

Пример. Пусть [ A=left( begin 1 &4 & -1 \ 3 & -6 & 7 end right) , ] [ B=left( begin 2 &1 & 0 \ 1 & 3 & 4 end right) , ] тогда [ A+B=left( begin 3 & 5 & -1 \ 4 & -3 & 11 end right) . ]

Пусть (A=>) – матрица типа ((m,n)), (lambda) – произвольное число. Тогда матрица (>) называется произведением числа (lambda ) на матрицу (A) и обозначается (lambda cdot A).

Пример. Пусть [ A=left( begin 1 &4 & -1 \ 7 & 5 & 2 \ 3 & -6 & 7 end right) , ] тогда [ 5A=left( begin 5 &20 & -5 \ 35 & 25 & 10 \ 15 & -30 & 35 end right) . ]

Как и в обычной, в матричной арифметике знак умножения иногда не указывают, так что выражения (ccdot A) и (cA) равноправны.

Пусть [ A=left( begin 2 & 3 \ 4 & 5 end right), B=left( begin 1 & -2 \ 3 & 4 end right). ]

[3A-2B=left( begin 4 & 13 \ 6 & 7 end right)]

Если для заданной матрицы (A) ее строки записать как столбцы, получим новую матрицу, которая называется транспонированной исходной, и обозначается (A^T).

Пример. Пусть [ A=left( begin 1 &4 & -1 & 4 \ 7 & 5 & 2 & 2\ 3 & -6 & 7 & 8 end right), ] тогда [ A^T=left( begin 1 &7 & 3 \ 4 & 5 & -6 \ -1 & 2 & 7 \ 4 &2 &8 end right) . ]

Подчеркнем, если матрица (A) имеет тип ((m,n)), то (A^T) имеет тип ((n,m)), так что эта операция, вообще говоря, меняет тип матрицы. В частности, если (A) была матрицей-столбцом, (A^T) будет матрицей-строкой той же длины. Поэтому из типографских соображений матрицу-столбец часто представляют в виде ((a_1,a_2,a_3. a_n)^T) (это выражение занимает меньше места).

Введенные операции обладают многими естественными арифметическими свойствами. Перечислим ряд из них.

1. Для любых матриц (A,B,C) одного типа ((A+B)+C=A+(B+C))(ассоциативность сложения).

2. Для любых матриц (A,B) одного типа (A+B=B+A) (коммутативность сложения).

3. Пусть ((m,n))-матрица (O) состоит из нулей. Такая матрица играет роль нуля при сложении матриц типа ((m,n)), (A+O=A), (0cdot A=O) для любой матрицы (A) того же типа.

4. Для любых чисел (c_1,c_2) и любой матрицы (A) верно ((c_1+c_2)A=c_1A+c_2A).

5. Для любых матриц (A,B) одного типа и любого числа (c) верно (c(A+B)=cA+cB).

6. Для любых чисел (c_1,c_2) и любой матрицы (A) верно ((c_1c_2)A=c_1(c_2A)).

7. Для любой матрицы (A) верно (1cdot A=A).

8. Для любых матриц (A,B) одного типа ((A+B)^T=A^T+B^T).

9. Для любого числа (c) и любой матрицы (A) верно: ((cA)^T=cA^T).

10. Для любой квадратной матрицы (detA=detA^T).

11. Для любой матрицы ((A^T)^T=A).

Рассмотрим сначала умножение матрицы-строки на матрицу столбец. Пусть (A=(a_1,a_2. a_n)), (B=(b_1,b_2. b_n)^T). Тогда

[ AB=a_1b_1+a_2b_2+. +a_nb_n=sum _^na_mb_m. quad quad(9) ]

Для того, чтобы было определено умножение между (A) и (B), необходимо, чтобы длина строки была равна длине столбца. Это условие называют условием согласования типов. Формулу (9) называют правилом умножения строчки на столбец.

Теперь обсудим общий случай. Пусть матрица (A) имеет тип ((m,n)), а матрица (B) имеет тип ((n,p)) (так что длина строки матрицы (A) совпадает с длиной столбца матрицы (B)). Тогда можно определить их произведение, матрицу (C), следующим образом: матрица (C) будет иметь тип ((m,p)), причем для вычисления ее элемента (C_), (1 leq i leq m, 1 leq k leq p), следует взять строку с номером (i) матрицы (A) и умножить на столбец с номером (k) матрицы (B), [ c_=a_b_<1k>+a_b_<2k>+. +a_b_=sum _^na_b_. ] Таким образом следует вычислить все (mp) элементов матрицы (C). Еще раз подчеркнем, что для того, чтобы можно было перемножать матрицы (A) и (B), их типы должны быть согласованы!

Пример. Пусть [ A=left( begin 1 &4 & -1 \ 3 & -6 & 7 end right) , B=left( begin 2 &1 \ 1 & 3 \ -3 &5 end right) . ]

В данном случае матрица (A) имеет тип (2,3), матрица (B) имеет тип (3,2), так что типы матриц согласнованы и в результате умножения (A) на (B) получим матрицу типа ((2,2)). Получаем: [ AB=left ( begin 1cdot 2 +4 cdot 1+(-1)cdot (-3) & 1cdot 1 +4 cdot 3+(-1)cdot 5\ 3cdot 2 +(-6) cdot 1+7cdot (-3) &3cdot 1 +(-6) cdot 3+7cdot 5 end right )= left( begin 9 & 8\ -21 & 20 end right). ]

Замечание. Для приведенных матриц произведение (BA) не определено – типы матриц (B) и (A)не согласованы. Это отражает общую ситуацию: результат произведения матриц зависит от порядка сомножителей (в отличие от обычной арифметики) – и даже может не существовать для одного выбора порядка сомножителей, существуя для другого.

Операция умножения матриц также обладает рядом естественных свойств. (Ниже считается, что типы матриц (A,B) согласованы, так что их можно перемножать).

6. Для квадратных матриц (A,B) одного типа (det(AB)=detA cdot detB).

7. Рассмотрим квадратную матрицу порядка (n), (E=diag<1,1,1. 1>). Такая матрица играет выделенную роль в умножении матриц: для любых матриц (A,B) имеем (EA=A), (BE=B). Матрица (E) называется единичной матрицей порядка (n). Согласно описанным выше результатам, (detE=1).

1. Умножить матрицы:

а) [ left( begin 2 & 1 \ 3 & 4 end right)cdot left( begin 1 & -1 \ 2 & 1 end right). ]

б) [ left( begin 3 & 1 & 1 \ 2 & 1 & 2 \ 1 & 2 & 1 end right)cdot left( begin 1 &1 & -1 \ 2 & -1 & 1 \ -1 & 2 & 1 end right). ]

2. Вычислить [ left( begin 3 & 2 \ -4 & -2 end right)^5. ]

3. Вычислить (AB-BA), если

а) [ A=left( begin 1 &2 & 3 \ 1 & -1 & 0 \ -1 & 2 & 1 end right), B=left( begin 4 & 2 & 3 \ – 1 & 1 & 3 \ 1 & 2 & 1 end right). ]

б) [ A=left( begin 2 &1 & 0 \ 1 & 1 & 2 \ 1 & 2 & 1 end right), B=left( begin 3 & 1 & -2 \ 1 & -1 & 3 \3 & 5 & 1 end right). ]

а) (f(A)), если (f(x)=x^2-3x+3), [ A=left( begin -1 & 3 & 2 \ 1 & -1 & 3 \ -1 & 2 & 1 end right). ]

б) (f(A)), если (f(x)=x^2+4x-2), [ A=left( begin 2 & 1 & 1 \ 3 & -1 & 2 \ -1 & 2 & 0 end right). ]

5. Показать, что каждая матрица второго порядка [ A=left( begin a & b \ c & d end right) ]

удовлетворяет уравнению [ x^2-(a+d)x+(ad-bc)=0. ]

В рамках обычной арифметики обсуждается решение числового уравнения [ ax=1, ] где (a) – заданное число. Если (a neq 0), это уравнение имеет единственное решение, которое обозначается (x=a^<-1>) и называется обратным к (a) числом.

Пусть (A) – заданная квадратная матрица порядка (n), можно рассмотреть матричное уравнение [ AX=E. quad quad(10) ]

Определение. Решение уравнения (ref) называется матрицей, обратной (A).

Теорема. Для того, чтобы существовала обратная (A) матрица, небходимо и достаточно, чтобы матрица (A) была невырожденной.

Обратную матрицу обозначают (A^<-1>).

Основные свойства обратной матрицы.

3. Если квадратные матрицы порядка (n) (A) и (B) невырождены, то (AB) тоже невырождена, у нее существует обратная матрица, причем ((AB)^<-1>=B^<-1>A^<-1>).

4. Для невырожденной квадратной матрицы (A) верно: ((A^<-1>)^<-1>=A).

5. Для невырожденной квадратной матрицы (A) верно: ((A^T)^<-1>=(A^<-1>)^T).

Докажите эти свойства обратной матрицы.

Для вычисления эелементов обратной матрицы существуют явные формулы.

Пусть (A) – квадратная невырожденная матрица порядка (n). Вычислим матрицу (D) – матрицу алгебраических дополнений, согласно соотношениям

Пример. Пусть (n=2), [ A=left( begin a & b \ c & d end right), ] (detA=ad-bc neq 0). Следуя (11), получаем: [ D=left( begin d & -c \ -b & a end right), ] так что [ A^<-1>=frac<1>left( begin d & -b \ -c & a end right). ]

Таким образом, для матрицы порядка 2 формулы для обратной матрицы достаточно простые. Для больших порядков формулы становятся существенно более громоздкими.

Найти обратную матрицу для матрицы

1. [ A=left( begin 2 &2 & 3 \ 1 & -1 & 0 \ -1 & 2 & 1 end right). ]

2. [ A=left( begin 2 &-1 & 0 \ 0 & 2 & -1 \ -1 & -1 & 1 end right). ]

3. [ A=left( begin 1 &1 & 1 \ 1 & 2 & 2 \ 2 & 3 & 4 end right). ]

Матричными уравнениями называются уравнения вида [ AX=G, quad quad(12)] [ XB=G, quad quad(13)] [ AXB=G, quad quad(14)] где матрицы (A,B,G) заданы и требуется построить матрицу (X). Мы будем здесь считать, что матрицы (A,B,G) – квадратные одного порядка. Решение этих уравнений нетрудно построить, если матрицы (A,B) невырождены, так что существуют их обратные (A^<-1>, B^<-1>). Умножая, например, уравнение (12) слева на матрицу (A^<-1>), получаем: [ A^<-1>(AX)=(A^<-1>A)X=EX=X=A^<-1>G. ] Умножая уравнение (13) справа на (B^<-1>), получаем: [ (XB)B^<-1>=X(BB^<-1>)=XE=X=GB^<-1>. ] Аналогично, умножая (14) слева на (A^<-1>) и справа на (B^<-1>), получим: [ X=A^<-1>GB^<-1>. ]

1. Найти решение матричного уравнения (12), если [ A=left( begin 2 & 6 \ -9 & 3 end right) , G=left( begin -26 & -50 \ 27 & -15 end right) . ]

2. Найти решение матричного уравнения (12), если [ A=left( begin 8 & -7 \ -5 & 4 end right) , G=left( begin 25 & -34 \ -16 & 22 end right) . ]

3. Найти решение матричного уравнения (13), если [ B=left( begin -8 & -5 \ -9 & 5 end right) , G=left( begin -20 & 30 \ -19 & 20 end right) . ]

4. Найти решение матричного уравнения (13), если [ B=left( begin 9 & 8 \ -3 & 7 end right) , G=left( begin -72 & 23 \ 0 & 58 end right) . ]

5. Найти решение матричного уравнения (14), если [ A=left( begin 4 & 2 \ 3 & -4 end right) , B=left( begin -1 & 2 \ -2 & -1 end right) , G=left( begin 20 & -50 \ 26 & 23 end right) . ]

6. Найти решение матричного уравнения (14), если [ A=left( begin -4 & -2 \ -3 & 3 end right) , B=left( begin 3 & 4 \ 4 & 3 end right) , G=left( begin 132 & 134 \ 18 & 24 end right) . ]

Умножение матрицы на число

Формула

Умножение матрицы на число – это операция над матрицей, в результате которой каждый её элемент умножается на дейсвительное или комплексное число. Выглядит математическим языком это так:

$$ B = lambda cdot A Rightarrow b_ = lambda a_ $$

Стоит заметить, что получаемая матрица $ B $ в результате должна получаться той же размерности, которой обладала начальная матрица $ A $. Так же можно обратить внимание на такой факт: $ lambda cdot A = A cdot lambda $, то есть можно менять местами множители и от этого произведение не изменится.

Будет полезным использовать операцию умножение матрицы на число при вынесении общего множителя за пределы матрицы. В этом случае каждый элемент матрицы делится на число $ lambda $, а сам он выносится перед матрицей.

Свойства

1. Дистрибутивный закон относительно матриц: $$ lambda cdot (A+B) = lambda A + lambda B $$Умножение суммы матриц на число можно заменить на сумму произведений каждой отдельной матрицы на данное число
2. Дистрибутивный закон относительно действительных (комплексных) чисел: $$ (lambda + mu) cdot A = lambda A + mu A $$ Умножение матрицы на сумму чисел можно заменить на сумму произведений каждого числа на матрицу
3. Ассоциативный закон: $$ lambda cdot (mu cdot A) = (lambda cdot mu) A $$ Удобно использовать если нужно вынести общий множитель из матрицы перед ней, при этом домножая уже стоящий перед ней коэффициент
4. Есть особое число $ lambda = 1 $, благодаря которому матрица остаётся неизменной $$ 1 cdot A = A cdot 1 = A $$
5. Умножение матрицы на ноль приводит к тому, что каждый элемент матриц обнуляется и матрица становится нулевой той же размерности, которой была изначально: $$ 0 cdot A = 0 $$

Примеры решений

Записываем математическую операцию умножения и заодно вспоминаем правило, которое гласит: матрица умножается на число поэлементно.

$$ lambda cdot A = 2 cdot begin 2&-1&4\0&9&3\-2&-3&5 end = begin 2cdot 2&2cdot (-1)&2cdot 4\2cdot 0&2 cdot 9&2cdot 3\2cdot (-2)&2cdot (-3)&2cdot 5 end = $$

В результате видим, что каждое число стоящее в матрицы удвоилось по отношению к начальному значению.

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Матрицы. Действия над матрицами. Свойства операций над матрицами. Виды матриц.

Матрицы. Действия над матрицами. Свойства операций над матрицами. Виды матриц.

Матрицы (и соответственно математический раздел – матричная алгебра) имеют важное значение в прикладной математике, так как позволяют записать в достаточно простой форме значительную часть математических моделей объектов и процессов. Термин “матрица” появился в 1850 году. Впервые упоминались матрицы еще в древнем Китае, позднее у арабских математиков.

Матрицей A=A_mn порядка m*n называется прямоугольная таблица чисел, содержащая m – строк и n – столбцов.

Элементы матрицы a_ij, у которых i=j, называются диагональными и образуют главную диагональ.

Для квадратной матрицы (m=n) главную диагональ образуют элементы a₁₁, a₂₂. a_nn .

Равенство матриц.

A=B, если порядки матриц A и B одинаковы и a_ij=b_ij (i=1,2. m; j=1,2. n)

Действия над матрицами.

1. Сложение матриц – поэлементная операция

2. Вычитание матриц – поэлементная операция

3. Произведение матрицы на число – поэлементная операция

4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B)

A_mk*B_kn=C_mn причем каждый элемент с_ij матрицы C_mn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B , т.е.

Покажем операцию умножения матриц на примере

5. Возведение в степень

m>1 целое положительное число. А – квадратная матрица (m=n) т.е. актуально только для квадратных матриц

6. Транспонирование матрицы А. Транспонированную матрицу обозначают A T или A’

Строки и столбцы поменялись местами

Пример

Свойства опрераций над матрицами

A+B=B+A

(A+B)+C=A+(B+C)

λ(A+B)=λA+λB

A(B+C)=AB+AC

(A+B)C=AC+BC

λ(AB)=(λA)B=A(λB)

A(BC)=(AB)C

(A’)’=A

(λA)’=λ(A)’

(A+B)’=A’+B’

(AB)’=B’A’

Виды матриц

1. Прямоугольные: m и n – произвольные положительные целые числа

2. Квадратные: m=n

3. Матрица строка: m=1. Например, (1 3 5 7 ) – во многих практических задачах такая матрица называется вектором

4. Матрица столбец: n=1. Например

5. Диагональная матрица: m=n и a_ij=0, если i≠j. Например

6. Единичная матрица: m=n и

7. Нулевая матрица: a_ij=0, i=1,2. m

j=1,2. n

8. Треугольная матрица: все элементы ниже главной диагонали равны 0.

9. Симметрическая матрица: m=n и a_ij=a_ji (т.е. на симметричных относительно главной диагонали местах стоят равные элементы), а следовательно A’=A

10. Кососимметрическая матрица: m=n и a_ij=-a_ji (т.е. на симметричных относительно главной диагонали местах стоят противоположные элементы). Следовательно, на главной диагонали стоят нули (т.к. при i=j имеем a_ii=-a_ii)

Ясно, A’=-A

11. Эрмитова матрица: m=n и a_ii=-ã_ii (ã_ji – комплексно – сопряженное к a_ji, т.е. если A=3+2i, то комплексно – сопряженное Ã=3-2i)